Wil jij online oefenen met het onderwerp Tangens en de verhoudingstabel? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!
Met Slimleren oefen je online op een leuke en efficiënte manier stof uit de les. Kom je ergens niet uit? Dan past het systeem automatisch het niveau aan en geeft handige tips. Zo loop je nooit meer vast en worden zelfs de moeilijkste onderwerpen een fluitje van een cent.
Hieronder zie je de theorie van het onderwerp Tangens en de verhoudingstabel, met Slimleren kun je vragen over dit onderwerp (en honderden andere onderwerpen) oefenen. Je krijgt direct feedback als je een vraag fout beantwoord en ziet gemakkelijk welke onderwerpen nog wat extra aandacht nodig hebben. Zo ben je altijd voorbereid op toetsen en ga je fluitend het schooljaar door.
Om makkelijk de horizontale verplaatsing, verticale verplaatsing, het hellingsgetal of de hellingshoek van een driehoek te kunnen uitrekenen met behulp van de tangens, kun je een verhoudingstabel gebruiken.
In deze theorie leggen we je uit hoe je met de tangens en deze verhoudingstabel werkt.
Als de hellingshoek en de verticale verplaatsing bekend zijn, kun je de de horizontale verplaatsing berekenen met behulp van een verhoudingstabel.
$$\mbox{Hellingsgetal} = \mbox{Tan(hellingshoek)=}\frac{\mbox{Verticale verplaatsing}}{\mbox{Horizontale verplaatsing}}$$
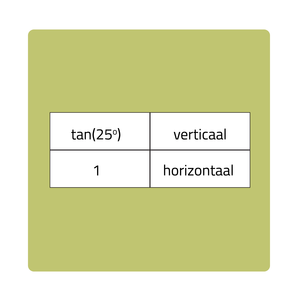
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} \mbox{Tan (hellingshoek)} & \mbox{Verticale verplaatsing} \T \\\hline 1 \T & \mbox{Horizontale verplaatsing} \end{array}$$
Bij een hellingshoek van bijvoorbeeld 25° en een verticale verplaatsing van 200 ziet de verhoudingstabel er zo uit:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} \mbox{Tan (25°)} & \mbox{200} \T \\\hline 1 \T & \mbox{Horizontale verplaatsing} \end{array}$$
Door kruislings vermenigvuldigen en delen zie je dat de horizontale verplaatsing als volgt te berekenen is: $$\mbox{horizontale verplaatsing} = \frac{200 \cdot 1} {\mbox{tan(25°)}} \approx 428,9$$
Met behulp van deze verhoudingstabel zou je ook de verticale verplaatsing kunnen berekenen als de horizontale verplaatsing en hellingshoek bekend zijn.
Een driehoek heeft een hellingshoek van 25° en een horizontale verplaatsing van 550.
Bereken de verticale verplaatsing en rond af op 2 decimalen nauwkeurig.
Uitwerking:
Maak een verhoudingstabel.
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} \mbox{Tan(25°)} & \mbox{Verticale verplaatsing} \T \\\hline 1 \T & 550 \end{array}$$ $$\mbox{verticale verplaatsing} = \frac{550 · \mbox{tan(25°)}}{1} = 256,47$$
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Daarnaast krijg je bij ieder fout gegeven antwoord direct een heldere uitleg hoe je de vraag het beste kunt oplossen. Zo leer je sneller en effectiever; dat is pas Slimleren!
Onderdeel worden van ons multidisciplinaire team? Dat kan! We zijn op zoek naar starters in de zorg, maar ook naar medisch specialisten en GZ-psychologen. Eén ding staat daarbij vast: je vult je functie anders in dan je gewend bent. Vind de vacature die bij je past en solliciteer!
Leren wordt leuker met Slimleren! Verzamel diamanten, speel mini-games en bereik gouden resultaten.
Slimleren is niet alleen leuker, maar ook veel goedkoper. Voor de prijs van 30 min bijles krijg je een hele maand Slimleren, al vanaf €8,95.
Met Slimleren houd je eenvoudig je voortgang bij en bereid je je optimaal voor op toetsen. Geen verrassingen meer!
Ervaar volledig adaptieve programma's door ons. Ons systeem speelt slim in op jouw uitdagingen. Leuker én effectiever leren!
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Onze programma's zijn gericht op leerlingen van groep 5 tot en met groep 8 van de basisschool en klas 1 tot en met klas 3 van de middelbare school. Of je nu wat moeite hebt met een bepaald vak, of juist vooruit wilt werken; Slimleren is er voor iedereen.
