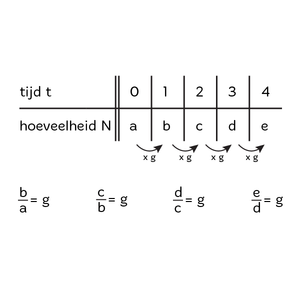
Exponentiële groei in een reeks vinden
Wil jij online oefenen met het onderwerp Exponentiële groei in een reeks vinden? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!