Uitdaging
De algemene vorm van een kwadratische formule is y = ax2 - bx + c. Waarbij $$a\neq 0$$. Als a 0 zou zijn, zou het geen kwadratische formule meer zijn. b en c zouden wel 0 kunnen zijn.
Voorbeelden van kwadratische formules zijn: y = x2 + 2x en y = x2 + 2x + 5. We kunnen y berekenen als x bekend is en andersom.
De grafiek van een kwadratische formule is een parabool. Elke parabool is symmetrisch, waarbij de symmetrieas door het midden en dus door de top van de parabool loopt. Je hebt twee soorten parabolen, namelijk berg- en dalparabolen.
In deze theorie leggen we je uit hoe je kunt zien of de grafiek van een kwadratische formule een berg- of een dalparabool is en hoe je coördinaten op de parabool kunt bepalen.
Methode
De algemene vorm van een kwadratische formule is y = ax2 - bx + c. Aan de formule kun je al direct zien welke vorm de grafiek zal hebben, namelijk:
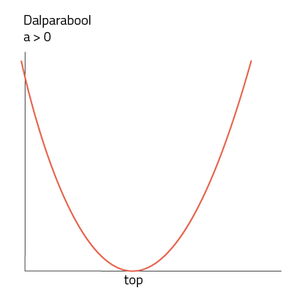
- Als a een positief getal is (a > 0), is de formule een dalparabool.
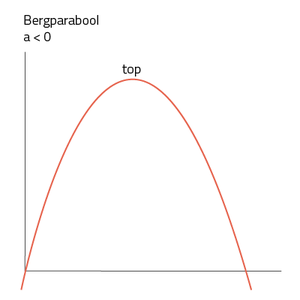
- Als a een negatief getal is (a < 0), is de formule een bergparabool.
Zowel dal- als een bergparabolen hebben een top. Bij een bergparabool is dit het hoogste punt van de grafiek, maar bij een dalparabool is de top het laagste punt van de grafiek. Als je de grafiek bij een kwadratische formule wilt tekenen, maak je eerst een tabel. In deze tabel zet je voor elke x de bijbehorende y-waarde.
Vervolgens kun je deze punten tekenen en teken je zo de parabool van de kwadratische formule.
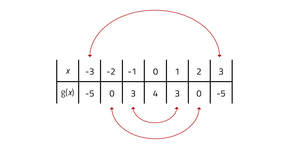
Omdat een parabool symmetrisch is, kun je bij het invullen van de tabel gebruik maken van de symmetrie. Wanneer je namelijk 2 keer dezelfde waarde voor y hebt gevonden, kan je stoppen met berekenen van de y-waarden.
Neem bijvoorbeeld de functie g(x) = -x2 + 4. Zoals je ziet in de tabel kan je stoppen met het berekenen van de y-waarden bij x = 1. Wanneer je gebruik maakt van de symmetrie weet je namelijk ook de y-waarden van x = 2 en x = 3.
Tevens weet je nu ook wat de top van de parabool is, namelijk het punt (0,4). Nadat je g(1) = 3 hebt gevonden weet je zeker dat het punt (0,4) de top van de parabool moet zijn. De top ligt namelijk altijd exact in het midden van 2 symmetrische punten.