Basis - machtsvergelijkingen oplossen

 

Machtsfunctie met een even macht

 

Machstfunctie met een oneven macht

 

Aantal oplossingen van machtsvergelijkingen

 

Derdemachtswortel op de rekenmachine

Uitdaging

We hebben eerder geleerd over het oplossen van kwadratische vergelijkingen. In deze vergelijkingen staat altijd een x², maar bijvoorbeeld niet een x³ of een x⁴. Vergelijkingen met een grotere macht dan een kwadraat erin noemen we vaak machtsvergelijkingen.

In deze theorie leer je hoe je een vergelijking met een macht groter dan 2 op kunt lossen.

Methode

Van de vergelijking x² = 16 weet je misschien al hoe je deze op kunt lossen. Neem aan beide kanten de wortel: x² = 16

$$\sqrt{x^2} = \sqrt{16}    \vee    \sqrt{x^2} = -\sqrt{16}$$

x = 4 ∨ x = -4

Een 'gewone' wortel, zoals die hierboven, is een tweedemachtswortel. Je zou deze ook kunnen noteren als $$\sqrt[2]{16}$$, maar die 2 laten we bij de tweedemachtswortel eigenlijk altijd weg.

$$\sqrt{16}$$ is dus hetzelfde als $$\sqrt[2]{16}$$

Naast tweedemachtswortels, bestaan er ook derdemachtswortels, vierdemachtswortels, enz. Deze heb je nodig bij het oplossen van een machtsvergelijking met een macht groter dan 2.

Een machtsvergelijking ziet er (in de meest eenvoudige vorm) zo uit:

$$x^n = a$$

Stel je hebt de vergelijking $$x^3 = 50$$. De macht in deze vergelijking is een 3, om deze uit de vergelijking weg te werken heb je een derdemachtswortel nodig. 

$$x^3 = 50$$

$$\sqrt[3]{x^3} = \sqrt[3]{50}$$

$$x= \sqrt[3]{50} \approx 3,68$$

Misschien ken je van veel tweedemachtswortels de uitkomsten inmiddels uit je hoofd, van een derdemachtswortel is dit een stukje lastiger. In de eerste afbeelding kun je zien welke knoppen op je rekenmachine je nodig hebt om een derdemachtswortel te berekenen. 

Op dezelfde manier kun je ook andere machten uit een vergelijking weg werken. Bijvoorbeeld:
$$x^9 = 512$$

$$\sqrt[9]{x^9} = \sqrt[9]{512}$$

$$x= \sqrt[9]{512} = 2$$

Zoals je je misschien herinnert heeft de vergelijking $$x^2 = a$$ twee oplossingen als a > 0.
(Zie het eerste voorbeeld van $$x^2 = 16$$)

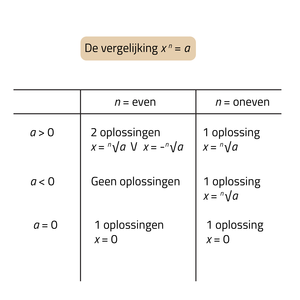
Bij machten hoger dan 2 heb je soortgelijke regels. Maar let goed op! Niet elke machtsvergelijking heeft 2 oplossingen. De volgende regels gelden voor de algemene vorm xⁿ = a.

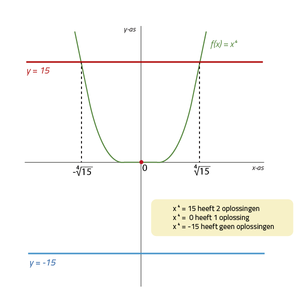
• Wanneer de macht n een even getal is én a > 0, zijn er 2 oplossingen.
• Wanneer de macht n een even getal is én a = 0 is er 1 oplossing, namelijk x = 0.
• Wanneer de macht n een even getal is én a < 0 zijn er geen oplossingen. 
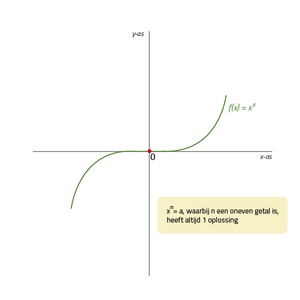
• Wanneer de macht n een oneven getal is, dan is er 1 oplossing.

Een voorbeeld van een machstfunctie met een even en een machtsfunctie met een oneven macht vindt je in de afbeeldingen hierboven. Een machtsfunctie met een even macht lijkt erg op een parabool, maar het is geen parabool.
Een machtsfunctie met een oneven macht heeft weer een hele andere vorm, namelijk een soort gedraaide 's'.