Uitdaging
Een variabele x kan een bepaalde waarde hebben, bijvoorbeeld x = 4. Het kan ook zo zijn dat de variabele x een waarde kan hebben die ergens tussenin ligt, bijvoorbeeld dat x groter is dan 2 maar kleiner dan 8, je schrijft dan 2 < x < 8. Je noemt dit ook wel een interval. Met een getallenlijn kan je zo'n interval weergeven. Je kan dan aflezen wat het interval van de x is.
Methode
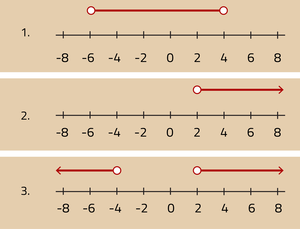
Er zijn een aantal verschillende soorten intervallen. In de afbeelding zie je 3 soorten intervallen.
- Een interval dat geheel op de getallenlijn ligt.
- Een interval dat met één grens op de getallenlijn ligt.
- Een interval dat met twee grenzen op de getallenlijn ligt.
Als je een interval moet beschrijven, geef je aan waartussen de waarde van x kan liggen.
- -6 < x < 4
- x > 2
- x < -4 ∨ x > 2