Wil jij online oefenen met het onderwerp Intervallen van ongelijkheden in grafieken? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!
Met Slimleren oefen je online op een leuke en efficiënte manier stof uit de les. Kom je ergens niet uit? Dan past het systeem automatisch het niveau aan en geeft handige tips. Zo loop je nooit meer vast en worden zelfs de moeilijkste onderwerpen een fluitje van een cent.
Hieronder zie je de theorie van het onderwerp Intervallen van ongelijkheden in grafieken, met Slimleren kun je vragen over dit onderwerp (en honderden andere onderwerpen) oefenen. Je krijgt direct feedback als je een vraag fout beantwoordt en ziet gemakkelijk welke onderwerpen nog wat extra aandacht nodig hebben. Zo ben je altijd voorbereid op toetsen en ga je fluitend het schooljaar door.
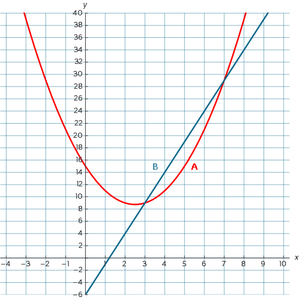
Grafieken van verschillende functies kunnen elkaar kruisen, zoals weergegeven is in het figuur. Grafiek A is op een bepaald moment kleiner dan grafiek B. Je kunt dit ook zien als een bepaald interval waarop grafiek A kleiner is dan grafiek B. De grenzen van het interval kun je vinden door de punten van de grafieken te vinden waarin zij elkaar snijden. Vervolgens kun je in de grafiek bekijken op aan welke kant van de snijpunten (op welk interval) grafiek A groter is dan grafiek B en aan welke kant van deze snijpunten (op welk interval) grafiek B groter is dan grafiek A.
In deze theorie leggen we je uit hoe dit precies werkt.
De grafieken in de afbeelding hebben de volgende formules: A = x2 - 5x + 15 en B = 5x - 6. Om de coördinaten van de snijpunten van deze lineaire en kwadratische formule te vinden volg je het volgende stappenplan.
Als je het interval wilt vinden waarin A < B dan los je eerst A = B op. Je vindt dan x = 3 en x = 7. Daarna kijk je in de grafiek of A tussen die waarden groter is of dat A juist kleiner is dan B. Je ziet in dit geval dat A tussen deze twee waarden kleiner is dan B. Je schrijft dit interval dus als volgt op: 3 < x < 7.
Als je het interval wilt vinden waarin A > B dan kijk je in de grafiek of A tussen die waarden groter is of dat A juist kleiner is dan B. Je ziet dat A tussen deze twee waarden kleiner is dan B. Je moet dus het interval hebben wat buiten deze waarden liggen. Je schrijft dit interval dus als volgt op: x < 3 ∨ x > 7.
In woorden kun je dan zeggen: A is groter dan B als x is kleiner dan 3 of x is groter dan 7.
Los de volgende ongelijkheid op:
f(x) = x2 + 2x + 6 > g(x) = -x + 16
Uitwerking
x2 + 2x + 6 > -x + 16
Haal eerst alle onderdelen naar de linkerkant van de vergelijking.
x2 + 3x - 10 > 0
Stel deze nieuwe vergelijking gelijk aan 0. Deze nieuwe vergelijking gebruik je om de snijpunten te bepalen.
x2 + 3x - 10 = 0
Los deze vergelijking op. Hier gebruik je de product-som-methode.
(x + 5)(x - 2)
x = -5 ∨ x = 2
Bekijk nu de originele grafieken (dus niet de nieuwe vergelijking). Je ziet dat tussen de snijpunten, g juist groter is dan f. Dus nu kan je deze ongelijkheid oplossen.
f > g geeft voor x < -5 ∨ x > 2
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Daarnaast krijg je bij ieder fout gegeven antwoord direct een heldere uitleg hoe je de vraag het beste kunt oplossen. Zo leer je sneller en effectiever; dat is pas Slimleren!
Onderdeel worden van ons multidisciplinaire team? Dat kan! We zijn op zoek naar starters in de zorg, maar ook naar medisch specialisten en GZ-psychologen. Eén ding staat daarbij vast: je vult je functie anders in dan je gewend bent. Vind de vacature die bij je past en solliciteer!
Leren wordt leuker met Slimleren! Verzamel diamanten, speel mini-games en bereik gouden resultaten.
Slimleren is niet alleen leuker, maar ook veel goedkoper. Voor de prijs van 30 min bijles krijg je een hele maand Slimleren, al vanaf €8,95.
Met Slimleren houd je eenvoudig je voortgang bij en bereid je je optimaal voor op toetsen. Geen verrassingen meer!
Ervaar volledig adaptieve programma's door ons. Ons systeem speelt slim in op jouw uitdagingen. Leuker én effectiever leren!
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Onze programma's zijn gericht op leerlingen van groep 5 tot en met groep 8 van de basisschool en klas 1 tot en met klas 3 van de middelbare school. Of je nu wat moeite hebt met een bepaald vak, of juist vooruit wilt werken; Slimleren is er voor iedereen.
