Uitdaging
Als er veel losse gegevens zijn, kan je deze overzichtelijk bundelen in een frequentietabel. Dit is bijvoorbeeld de frequentietabel van het aantal broeken van van een groep van 16 vriendinnen:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} \mbox{Aantal broeken} & 1 & 2 & 3 & 4 \T \\\hline \mbox{Frequentie} \T & 5 & 6 & 3 & 2 \end{array}$$
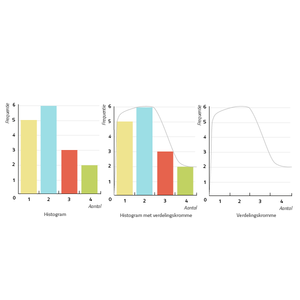
Bij deze frequentietabellen kan door middel van een histogram een globale grafiek worden gemaakt, een verdelingskromme. Zo kan je in 1 oogopslag de informatie zien. Erg handig dus!
Een verdelingskromme komt voor in verschillende vormen. Wat deze vormen zijn en wat de eigenschappen daarvan zijn bespreken we in deze theorie.
Methode
Als je een lijn trekt langs de toppen van de histogram staven, dan krijg je een globale grafiek van de verdeling. Dit noem je een verdelingskromme. In zo'n verdelingskromme zijn de centrummaten, het gemiddelde, de mediaan en de modus, verwerkt. De top van zo'n grafiek ligt bij de modus, want dat is de waarde met de hoogste frequentie.
In de wiskunde krijg je regelmatig te maken met vier verschillende vormen/soorten verdelingskrommen, zie ook de afbeeldingen:
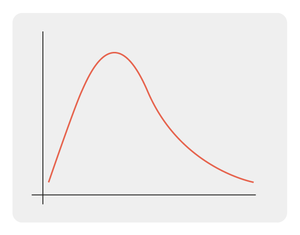
Rechtsscheef:
- Kleinste centrummaat: modus
- Grootste centrummaat: gemiddelde
- De mediaan ligt tussen de modus en het gemiddelde in
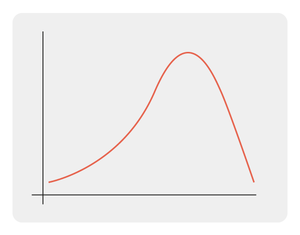
Linksscheef:
- Kleinste centrummaat: gemiddelde
- Grootste centrummaat: modus
- De mediaan ligt tussen de modus en het gemiddelde in
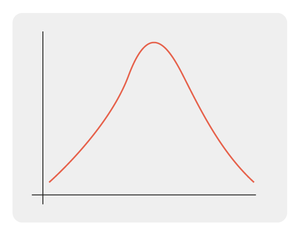
Symmetrisch:
- De 3 centrummaten zijn gelijk
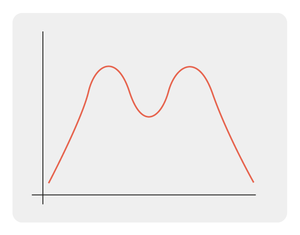
Tweedelig:
- Er zijn 2 frequentie pieken.
- Let op, dit mag je geen modus noemen, want er is alleen een modus als er 1 grootste frequentie is.