Wil jij online oefenen met het onderwerp Bijzondere kwadratische ongelijkheden? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!
Met Slimleren oefen je online op een leuke en efficiënte manier stof uit de les. Kom je ergens niet uit? Dan past het systeem automatisch het niveau aan en geeft handige tips. Zo loop je nooit meer vast en worden zelfs de moeilijkste onderwerpen een fluitje van een cent.
Hieronder zie je de theorie van het onderwerp Bijzondere kwadratische ongelijkheden, met Slimleren kun je vragen over dit onderwerp (en honderden andere onderwerpen) oefenen. Je krijgt direct feedback als je een vraag fout beantwoordt en ziet gemakkelijk welke onderwerpen nog wat extra aandacht nodig hebben. Zo ben je altijd voorbereid op toetsen en ga je fluitend het schooljaar door.
Een kwadratische ongelijkheid heeft de vorm van een kwadratische vergelijking, maar dan zijn de linker- en rechter kant van de vergelijking niet aan elkaar gelijk, maar juist ongelijk aan elkaar.
Ongelijkheden kunnen worden aangegeven met de tekens kleiner dan < en groter dan >. Hoe je deze vergelijkingen kunt oplossen leggen we je uit in deze theorie.
Kwadratische ongelijkheden kunnen verschillende grafieken tot stand brengen. Als (volgens de abc-formule) a > 0, dan is de grafiek een dalparabool en als a < 0, dan is de grafiek een bergparabool.
Het oplossen van een bijzondere vergelijking kunnen we doen met de volgende stappen.
Los op.
a. x2 - 2x + 6 > 0
b. 2x2 + 3x - 4 < 0
Uitwerking
a. Stap 1: Stel de vergelijking gelijk aan 0.
x2 - 2x + 6 = 0
Stap 2: Indien zelf geen oplossing te vinden, gebruik abc-formule.
a = 1, b = -2, c = 6
D = -22 - 4 · 1 · 6 = -20
Stap 3: Bereken de oplossing.
D < 0, dus er zijn geen oplossingen.
Stap 4: Bepaal of de vergelijking een dal- of bergparabool is en kijk waar de grafiek de x-as snijdt.
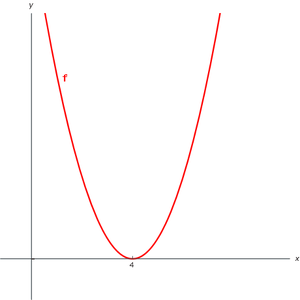
De grafiek is een dalparabool, want a > 0, die de x-as niet snijdt.
b. Stap 1: Stel de vergelijking gelijk aan 0.
2x2 + 3x - 4 = 0
Stap 2: Indien zelf geen oplossing te vinden, gebruik abc-formule.
a = 2, b = 3, c = -4
D = 32 - 4 · 2 · -4 = 41
Stap 3: Bereken de oplossing.
D > 0, er zijn 2 oplossingen.
$$x=\frac{-3 - \sqrt{41}}{2 · 2} = -2,4$$
$$x=\frac{-3 + \sqrt{41}}{2 · 2} = 0,9$$
Stap 4: Bepaal of de vergelijking een dal- of bergparabool is en kijk waar de grafiek de x-as snijdt.
De grafiek is een dalparabool want a > 0 en snijdt de x-as in de punten (-2,4, 0) en (0,9, 0).
Stap 5: Noteer je antwoord voor wanneer de vergelijking kleiner is dan 0.
2x2 + 3x - 4 < 0 voor x < -2,4 en x > 0,9
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Daarnaast krijg je bij ieder fout gegeven antwoord direct een heldere uitleg hoe je de vraag het beste kunt oplossen. Zo leer je sneller en effectiever; dat is pas Slimleren!
Onderdeel worden van ons multidisciplinaire team? Dat kan! We zijn op zoek naar starters in de zorg, maar ook naar medisch specialisten en GZ-psychologen. Eén ding staat daarbij vast: je vult je functie anders in dan je gewend bent. Vind de vacature die bij je past en solliciteer!
Leren wordt leuker met Slimleren! Verzamel diamanten, speel mini-games en bereik gouden resultaten.
Slimleren is niet alleen leuker, maar ook veel goedkoper. Voor de prijs van 30 min bijles krijg je een hele maand Slimleren, al vanaf €8,95.
Met Slimleren houd je eenvoudig je voortgang bij en bereid je je optimaal voor op toetsen. Geen verrassingen meer!
Ervaar volledig adaptieve programma's door ons. Ons systeem speelt slim in op jouw uitdagingen. Leuker én effectiever leren!
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Onze programma's zijn gericht op leerlingen van groep 5 tot en met groep 8 van de basisschool en klas 1 tot en met klas 3 van de middelbare school. Of je nu wat moeite hebt met een bepaald vak, of juist vooruit wilt werken; Slimleren is er voor iedereen.
