Uitdaging
Gelijkvormige driehoeken zijn driehoeken die qua vorm identiek zijn aan elkaar en waarvan de hoeken gelijk zijn. Om gelijkvormig te zijn, moeten er dus drie hoeken even groot zijn als de drie hoeken van de andere driehoek.
In de praktijk betekent dit echter dat zodra er twee paar gelijke hoeken zijn, dat er gesproken kan worden van gelijkvormige driehoeken, want als er twee paar hoeken gelijk zijn, is het derde paar hoeken ook altijd gelijk. Dus: voor gelijkvormigheid bij driehoeken moeten er twee gelijke hoekparen zijn.
Om gelijkvormigheid vast te kunnen stellen kun je soms gebruik maken van de stellingen over overstaande hoeken bij snijdende lijnen, F-hoeken bij evenwijdige lijnen en Z-hoeken bij evenwijdige lijnen. In deze theorie gaan we hier verder op in.
Methode
Als je wilt weten of twee driehoeken gelijkvormig zijn, moet je dus nagaan of je twee hoekenparen kunt vinden die gelijk zijn aan elkaar. Als deze bestaan, dan zijn de driehoeken gelijkvormig en dus kun je een verhoudingstabel gebruiken om de zijden te berekenen. In de volgende situaties is er sprake van gelijke hoeken:
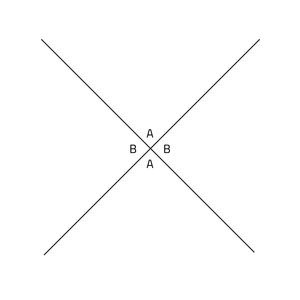
- Overstaande hoeken bij snijdende lijnen
- F-hoeken bij evenwijdige lijnen
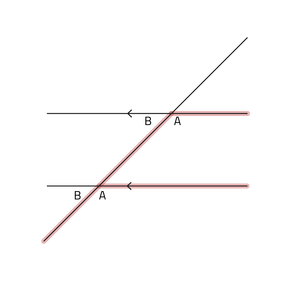
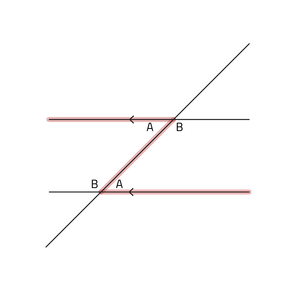
- Z-hoeken bij evenwijdige lijnen
Je kan de F-figuur en Z-figuur dus als hulpmiddel gebruiken om erachter te komen welke hoeken gelijkvormig zijn. Bekijk de afbeelding van de Z-hoek, de hoeken met de zelfde letters zijn gelijk. Als er een F-hoek te ontdekken is dan weet je ook dat een aantal hoeken gelijk zijn. Deze eigenschappen over gelijke hoeken, geven je nuttige informatie als er gevraagd wordt onbekende hoeken te berekenen.
Nadat je de gelijke hoeken hebt gevonden kan je de onbekende zijden vinden door middel van een verhoudingstabel.