Uitdaging
Kansen worden gebruikt om een indruk te geven van de waarschijnlijkheid van een gebeurtenis. Je kunt niet met zekerheid zeggen dat iets gaat gebeuren, maar er zou een grotere kans kunnen zijn op de ene gebeurtenis dan op de andere. Zo heb je bijvoorbeeld als je met 2 dobbelstenen gooit een grotere kans op het gooien van totaal 6 dan totaal 10.
In deze theorie gaan we verder in op het berekenen van een kans.
Methode
Om kansen te kunnen berekenen is het makkelijker als je een overzicht hebt van alle mogelijke uitkomsten.
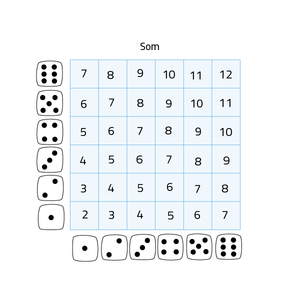
Kijk naar de afbeelding van het dobbelstenen rooster. Bij het gooien van 2 dobbelstenen is het handig om een 6 bij 6 rooster te tekenen. In totaal zijn er dan 36 uitkomsten. Het rooster geeft alle mogelijke uitkomsten weer van de som van de getallen op de dobbelstenen.
Stel we willen weten: Hoe groot de kans is dat je 4 gooit wanneer je 2 dobbelstenen gebruikt?
$$\mbox{Kans =} \frac{\mbox{Aantal gunstige uitkomsten}}{\mbox{Aantal mogelijke uitkomsten}}$$
Het aantal gunstige uitkomsten = het aantal uitkomsten dat 4 oplevert.
In dit geval zijn er 3 uitkomsten met als som 4. Het totale aantal mogelijke uitkomsten = 36.
Antwoord: $$\mbox{Kans =} \frac{3}{36} = 0,083$$. Een kans noteer je als P(gebeurtenis). Kansen rond je meestal af op 3 decimalen.
De kans om bij het gooien met 2 dobbelstenen 'som 4' te krijgen is P(som 4) = 0,083.