Wil jij online oefenen met het onderwerp Basis 1 - werken met lineaire formules? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!
Met Slimleren oefen je online op een leuke en efficiënte manier stof uit de les. Kom je ergens niet uit? Dan past het systeem automatisch het niveau aan en geeft handige tips. Zo loop je nooit meer vast en worden zelfs de moeilijkste onderwerpen een fluitje van een cent.
Hieronder zie je de theorie van het onderwerp Basis 1 - werken met lineaire formules, met Slimleren kun je vragen over dit onderwerp (en honderden andere onderwerpen) oefenen. Je krijgt direct feedback als je een vraag fout beantwoordt en ziet gemakkelijk welke onderwerpen nog wat extra aandacht nodig hebben. Zo ben je altijd voorbereid op toetsen en ga je fluitend het schooljaar door.
In de wiskunde wordt er veel gewerkt met formules. Een veel voorkomende formule is: y = ax + b. Dit is de algemene vorm van een lineaire formule en binnen deze formule bestaat een lineair verband tussen x en y. Dat betekent dat als de waarde van x met even grote stapjes omhoog/omlaag gaat, dat de waarde van y dan ook met even grote stapjes (die groter of kleiner kunnen zijn) omhoog/omlaag gaat.
In deze theorie leggen we je uit hoe je kunt rekenen met lineaire formules.
De richtingscoëfficiënt en de constante
De grafiek van de lineaire formule y = ax + b is een lijn met de volgende gegevens:
De richtingscoëfficiënt a geeft aan in welke mate de lijn stijgt of daalt en is te berekenen met de volgende formule:
$$\mbox{richtingscoëfficiënt }a=\frac{\mbox{verticale afstand}}{\mbox{horizontale afstand }}$$
De constante b brengt de grafiek omlaag of omhoog. Het geeft aan waar de grafiek de y-as snijdt. Het snijpunt met de y-as is altijd bij x = 0. Je kunt b dus berekenen door voor x = 0 de formule uit te rekenen.
Formule bepalen van een lijn
Indien er een lijn wordt gegeven en je wilt daar de formule bij weten, dankan dat aan de hand van de volgende stappen:
Voorbeeld
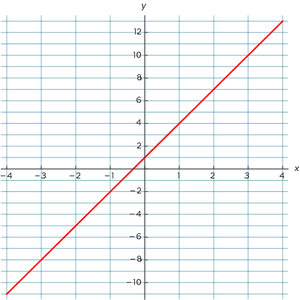
In het assenstelsel met de rode grafiek kun je zien dat de lijn met elk blokje naar rechts tegelijkertijd 3 blokjes omhoog gaat. De richtingscoëfficiënt a is dus 3. Verder is te zien dat op x = 0 de lijn de y-as snijdt op y = 1. Het snijpunt met de y-as is dus (0,1). Dit betekent direct ook dat b = 1.
De lineaire vergelijking is dus y = 3x + 1.
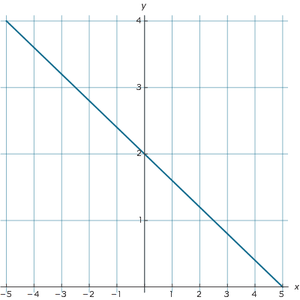
Bij de rode grafiek kun je duidelijk zien hoeveel de lijn stijgt. Maar helaas is dit niet altijd direct af te lezen. Zoals bijvoorbeeld te zien is in de blauwe grafiek. Hier kun je niet aflezen hoeveel de grafiek daalt per stapje naar rechts. Je kunt dit wel berekenen. Hiervoor zoek je 2 punten op de grafiek die je wel duidelijk kunt aflezen. Je ziet dat de blauwe grafiek precies door punt (0,2) en punt (5,0) gaat. Vervolgens bereken je de richtingscoëfficiënt met de formule:
$$\mbox{Richtingscoëfficiënt } a = \frac{\mbox{verticale afstand}}{\mbox{horizontale afstand}} = -\frac{\mbox{2}}{\mbox{4}} = -0,4$$.
Let op: deze richtingscoëfficiënt is negatief, omdat het om een dalende lijn gaat. Je zet er dus een min voor.
Vind de formule van de grafiek.
Uitwerking
De oplossing is door naar meerdere blokjes te kijken. In de grafiek daalt de lijn van (0,2) naar (5,0). Dit betekent dat de lijn 5 blokjes naar rechts en 2 blokjes omlaag gaat.
Om nu de richtingscoëfficiënt te bepalen deel je het aantal blokjes naar beneden door het aantal blokjes naar rechts.
$$\mbox{Richtingscoëfficiënt} = \frac{\mbox{verticale afstand}}{\mbox{horizontale afstand}}= \frac{2}{5} = 0,4$$.
De lijn daalt, dus is de richtingscoëfficiënt negatief. a = -0,4.
Je kunt zien dat de grafiek de y-as snijdt op (2,0), dus b = 2.
Nu kun je de formule opstellen, namelijk: y = -0,4x + 2.
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Daarnaast krijg je bij ieder fout gegeven antwoord direct een heldere uitleg hoe je de vraag het beste kunt oplossen. Zo leer je sneller en effectiever; dat is pas Slimleren!
Onderdeel worden van ons multidisciplinaire team? Dat kan! We zijn op zoek naar starters in de zorg, maar ook naar medisch specialisten en GZ-psychologen. Eén ding staat daarbij vast: je vult je functie anders in dan je gewend bent. Vind de vacature die bij je past en solliciteer!
Leren wordt leuker met Slimleren! Verzamel diamanten, speel mini-games en bereik gouden resultaten.
Slimleren is niet alleen leuker, maar ook veel goedkoper. Voor de prijs van 30 min bijles krijg je een hele maand Slimleren, al vanaf €8,95.
Met Slimleren houd je eenvoudig je voortgang bij en bereid je je optimaal voor op toetsen. Geen verrassingen meer!
Ervaar volledig adaptieve programma's door ons. Ons systeem speelt slim in op jouw uitdagingen. Leuker én effectiever leren!
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Onze programma's zijn gericht op leerlingen van groep 5 tot en met groep 8 van de basisschool en klas 1 tot en met klas 3 van de middelbare school. Of je nu wat moeite hebt met een bepaald vak, of juist vooruit wilt werken; Slimleren is er voor iedereen.
