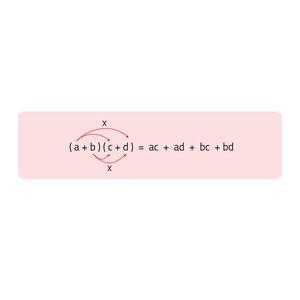Uitdaging
Als er haakjes in een vergelijking zitten, moet je deze als eerste wegwerken. Er zijn verschillende regels om haakjes weg te werken.
Hier oefen je met het wegwerken van haakjes van sommen met vorm:
a (b + c) en (a + b)(c + d).
Methode
De twee hoofdregels voor het wegwerken van haakjes zijn de volgende:
- a (b + c) = ab + ac
- (a + b)(c + d) = ac + ad + bc + bd
a (b + c) = ab + ac
a (b + c) betekent hetzelfde als a · (b + c). Omdat b + c tussen haakjes staat, moet je a vermenigvuldigen met (b + c) als geheel. Dit doe je door a te vermenigvuldigen met het eerste deel binnen de haakjes en vervolgens met het tweede deel binnen de haakjes.
In dit geval vermenigvuldig je a dus met b én met c.
a (b + c) = a · b en a · c = ab + ac
(a + b)(c + d) = ac + ad + bc + bd
Zoals je in de vorige vergelijking a met b én c vermenigvuldigde, zo moet je in dit geval a met c én d vermenigvuldigen en b met c én d vermenigvuldigen. In de figuur zie je hoe je vermenigvuldigt.
(a + b)(c + d) = a · c + a · d + b · c + b · d = ac + ad + bc + bd