Wil jij online oefenen met het onderwerp Oppervlakte van een parallellogram? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!
Met Slimleren oefen je online op een leuke en efficiënte manier stof uit de les. Kom je ergens niet uit? Dan past het systeem automatisch het niveau aan en geeft handige tips. Zo loop je nooit meer vast en worden zelfs de moeilijkste onderwerpen een fluitje van een cent.
Hieronder zie je de theorie van het onderwerp Oppervlakte van een parallellogram, met Slimleren kun je vragen over dit onderwerp (en honderden andere onderwerpen) oefenen. Je krijgt direct feedback als je een vraag fout beantwoord en ziet gemakkelijk welke onderwerpen nog wat extra aandacht nodig hebben. Zo ben je altijd voorbereid op toetsen en ga je fluitend het schooljaar door.
Een parallellogram is een vierhoek met bijzondere eigenschappen. De overstaande zijden van een parallellogram zijn evenwijdig en even lang. De overstaande hoeken zijn even groot en de diagonalen delen elkaar middendoor.
Van een parallellogram kun je ook de oppervlakte berekenen. In deze theorie behandelen we hoe je dat precies kunt doen.
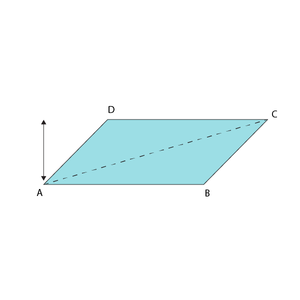
Als je een diagonaal door een parallellogram tekent zie je dat deze uit twee driehoeken bestaat. Anders gezegd: de diagonaal verdeelt een parallellogram in twee driehoeken.
$$\mbox{Oppervlakte driehoek in parallellogram = }\frac{1}{2} · \mbox{zijde} · \mbox{bijbehorende hoogte}$$
Aangezien er twee dezelfde driehoeken in een parallellogram passen, kun je de oppervlakte van een parallellogram berekenen door de oppervlakte van een driehoek te vermenigvuldigen met 2. Dan krijg je dus:
$$\mbox{Oppervlakte parallellogram = zijde · bijbehorende hoogte}$$
Let op: de bijbehorende hoogte ligt loodrecht op de zijde.
De zijde van een parallellogram is 8 cm en de bijbehorende hoogte is 4 cm. Bereken de oppervlakte.
Uitwerking
Oppervlakte parallellogram = 8 · 4 = 32 cm2
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Daarnaast krijg je bij ieder fout gegeven antwoord direct een heldere uitleg hoe je de vraag het beste kunt oplossen. Zo leer je sneller en effectiever; dat is pas Slimleren!
Onderdeel worden van ons multidisciplinaire team? Dat kan! We zijn op zoek naar starters in de zorg, maar ook naar medisch specialisten en GZ-psychologen. Eén ding staat daarbij vast: je vult je functie anders in dan je gewend bent. Vind de vacature die bij je past en solliciteer!
Leren wordt leuker met Slimleren! Verzamel diamanten, speel mini-games en bereik gouden resultaten.
Slimleren is niet alleen leuker, maar ook veel goedkoper. Voor de prijs van 30 min bijles krijg je een hele maand Slimleren, al vanaf €8,95.
Met Slimleren houd je eenvoudig je voortgang bij en bereid je je optimaal voor op toetsen. Geen verrassingen meer!
Ervaar volledig adaptieve programma's door ons. Ons systeem speelt slim in op jouw uitdagingen. Leuker én effectiever leren!
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Onze programma's zijn gericht op leerlingen van groep 5 tot en met groep 8 van de basisschool en klas 1 tot en met klas 3 van de middelbare school. Of je nu wat moeite hebt met een bepaald vak, of juist vooruit wilt werken; Slimleren is er voor iedereen.
