Uitdaging
De middelloodlijn staat loodrecht op een lijnstuk staat en deelt deze door het midden. De omgeschreven cirkel gaat door alle hoekpunten van een driehoek.
Je kunt de omgeschreven cirkel tekenen met behulp van de middelloodlijnen van de driehoek. Hoe dat precies werkt wordt in deze theorie besproken.
Methode
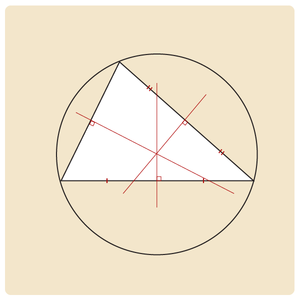
De drie middelloodlijnen van de zijden van iedere driehoek snijden elkaar altijd in één punt, punt M. Dit punt ligt precies even ver van alle hoeken van de driehoek. Dit punt is het middelpunt van een cirkel die door alle hoekpunten van de driehoek gaat: dit is de omgeschreven cirkel van de driehoek.
Als je de omgeschreven cirkel van een driehoek wilt tekenen, teken je eerst de middelloodlijnen van de driehoek. Zet vervolgens je passer in het snijpunt van de middelloodlijnen. De afstand tussen de benen van de passer is de afstand tussen het snijpunt en een hoek. Als je je passer goed hebt gezet, kun je de omgeschreven cirkel tekenen.
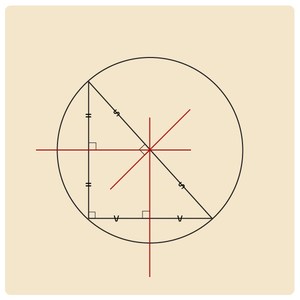
Als de driehoek een rechte hoek (90°) heeft, dan ligt het snijpunt van de middelloodlijnen (en dus ook het middelpunt van de omgeschreven cirkel) op de schuine zijde van de driehoek.