Uitdaging
Lichtstralen kunnen zorgen voor een projectie van een voorwerp. In deze theorie leer je met behulp van verhoudingstabellen hoe je kunt rekenen met projecties.
Methode
Wanneer de lichtstralen uit 1 punt komen spreek je van centrale projectie.
Wanneer de lichtstralen evenwijdig aan elkaar zijn spreek je van parallelle projectie.
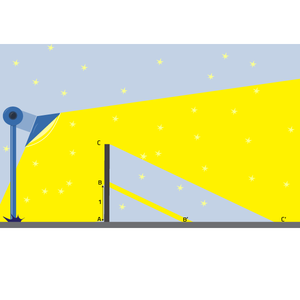
Bij centrale projectie zijn de schaduw van het voorwerp en het voorwerp zelf in verhouding met elkaar. Kijk naar de afbeelding met de plank en de lichtbron. Het licht gaat door de het gat in de plank en langs de bovenkant van de plank.
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} \mbox{Lengte plank} &AB & BC & AC \T \\\hline \mbox{Lengte schaduw}& AB' & B'C' & AC' \end{array}$$
Als gegeven is dat de afstand AB' = 3, afstand B'C' = 9 zijn, dan kun je met deze informatie de totale lengte van de balk, AC, uitrekenen.
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 1 & BC & AC \T \\\hline 3 & 9 & 12 \end{array}$$
AB' · AC = AB · AC'
$$AC = \frac{1 · 12}{3} = 4$$
Bij parallelle projectie zijn de lichtstralen evenwijdig aan elkaar.
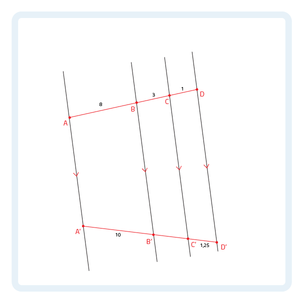
Kijk naar de afbeelding. De lichtstralen zijn evenwijdig aan elkaar, dus kun je een verhoudingstabel maken:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} AB & BC & CD \T \\\hline A'B' & B'C' & C'D' \end{array}$$
Vul nu de waardes in:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 8 & 3 & 1 \T \\\hline 10 & B'C' & 1,25 \end{array}$$
B'C' · AB = A'B' · BC $$B'C = \frac{3 · 10}{8} = 3,75$$