Wil jij online oefenen met het onderwerp Introductie van de Stelling van Pythagoras? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!
Met Slimleren oefen je online op een leuke en efficiënte manier stof uit de les. Kom je ergens niet uit? Dan past het systeem automatisch het niveau aan en geeft handige tips. Zo loop je nooit meer vast en worden zelfs de moeilijkste onderwerpen een fluitje van een cent.
Hieronder zie je de theorie van het onderwerp Introductie van de Stelling van Pythagoras, met Slimleren kun je vragen over dit onderwerp (en honderden andere onderwerpen) oefenen. Je krijgt direct feedback als je een vraag fout beantwoordt en ziet gemakkelijk welke onderwerpen nog wat extra aandacht nodig hebben. Zo ben je altijd voorbereid op toetsen en ga je fluitend het schooljaar door.
Soms komt het voor dat je de lengte van de zijde van een rechthoekige driehoek wilt weten, maar geen liniaal of meetlat hebt. De wiskundige Pythagoras heeft ontdekt dat als je de lengte van twee zijden weet, dat je de derde zijde gemakkelijk kunt uitrekenen.
Misschien heb je weleens gehoord van a2 + b2 = c2 ? In deze theorie leggen we uit wat de Stelling van Pythagoras is en wat je ermee kunt doen.
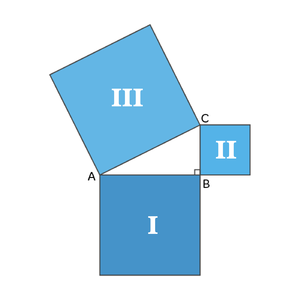
De bekende wiskundige Pythagoras heeft ontdekt dat een rechthoekige driehoek speciale eigenschappen heeft. Aan elke zijde van een rechthoekige driehoek kun je namelijk een vierkant maken. Dit kun je in de afbeelding zien.
De oppervlakte van de twee kleine vierkanten samen is gelijk aan de oppervlakte van het grote vierkant.
oppervlakte I + oppervlakte II = oppervlakte III
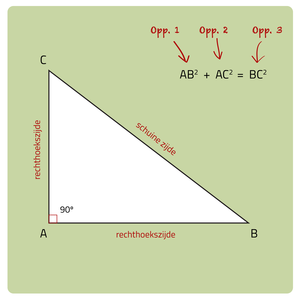
Let op! Dit geldt alleen voor rechthoekige driehoeken. Deze driehoeken hebben dus één rechte hoek (van 90°). De zijden die de benen zijn van deze rechte hoek worden rechthoekszijden genoemd. De zijde tegenover de rechte hoek noemen we de schuine zijde. In deze rechthoekige driehoek geldt:
Stelling van Pythagoras
Oppervlakte I + oppervlakte II = oppervlakte III. Hieruit volgt de stelling van Pythagoras: AB2 + BC2 = AC2
Let wel op dat de letters ook anders kunnen zijn. Dit kun je zien in de tweede rechthoekige driehoek. Hier wordt de stelling van Pythagoras AC2 + AB2 = BC2.
Onthoudt daarom de stelling van Pythagoras in de algemene vorm:
(ene rechthoekszijde)2 + (andere rechthoekszijde)2 = (schuine zijde)2
Of ook wel bekend als: a2 + b2 = c2, waarbij a en b de rechthoekszijden zijn en c de schuine zijde is.
a. In de figuur zie je een rechthoekige driehoek die wordt ingesloten door vierkanten. Bereken de oppervlakte van het kleine vierkant.
b. Van $$\Delta{KLM}$$ is $$\angle K = 90°$$. Schrijf voor deze driehoek de stelling van Pythagoras op.
Uitwerking
a. Oppervlakte l + oppervlakte II = oppervlakte III. Waarbij l en ll de 2 kleinste vierkanten zijn en lll de grootste is. Je wilt de oppervlakte van de kleinste berekenen, dus dan wordt het: oppervlakte I = oppervlakte IIl - oppervlakte II.
Oppervlakte kleinste vierkant = 30 - 20 = 10.
b. Als $$\angle K$$ de rechte hoek is, dan zijn zijden KL en KM de rechthoekszijden en zijde LM de schuine zijde. De stelling van Pythagoras wordt dan:
KL2 + KM2 = LM2.
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Daarnaast krijg je bij ieder fout gegeven antwoord direct een heldere uitleg hoe je de vraag het beste kunt oplossen. Zo leer je sneller en effectiever; dat is pas Slimleren!
Onderdeel worden van ons multidisciplinaire team? Dat kan! We zijn op zoek naar starters in de zorg, maar ook naar medisch specialisten en GZ-psychologen. Eén ding staat daarbij vast: je vult je functie anders in dan je gewend bent. Vind de vacature die bij je past en solliciteer!
Leren wordt leuker met Slimleren! Verzamel diamanten, speel mini-games en bereik gouden resultaten.
Slimleren is niet alleen leuker, maar ook veel goedkoper. Voor de prijs van 30 min bijles krijg je een hele maand Slimleren, al vanaf €8,95.
Met Slimleren houd je eenvoudig je voortgang bij en bereid je je optimaal voor op toetsen. Geen verrassingen meer!
Ervaar volledig adaptieve programma's door ons. Ons systeem speelt slim in op jouw uitdagingen. Leuker én effectiever leren!
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Onze programma's zijn gericht op leerlingen van groep 5 tot en met groep 8 van de basisschool en klas 1 tot en met klas 3 van de middelbare school. Of je nu wat moeite hebt met een bepaald vak, of juist vooruit wilt werken; Slimleren is er voor iedereen.
