Wil jij online oefenen met het onderwerp Bach-stelling en hpq-stelling in een driehoek? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!
Met Slimleren oefen je online op een leuke en efficiënte manier stof uit de les. Kom je ergens niet uit? Dan past het systeem automatisch het niveau aan en geeft handige tips. Zo loop je nooit meer vast en worden zelfs de moeilijkste onderwerpen een fluitje van een cent.
Hieronder zie je de theorie van het onderwerp Bach-stelling en hpq-stelling in een driehoek, met Slimleren kun je vragen over dit onderwerp (en honderden andere onderwerpen) oefenen. Je krijgt direct feedback als je een vraag fout beantwoordt en ziet gemakkelijk welke onderwerpen nog wat extra aandacht nodig hebben. Zo ben je altijd voorbereid op toetsen en ga je fluitend het schooljaar door.
We kunnen de oppervlakte van $$\Delta{ABC}$$ berekenen door $$\frac{1}{2}\cdot a \cdot b $$. Ook kunnen we gebruik maken van de bach-stelling en de hpq-stelling.
In deze theorie leggen we je uit wat deze stellingen zijn en hoe je ermee kunt rekenen.
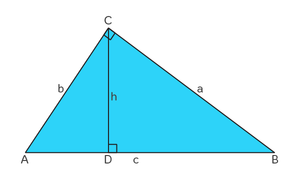
De oppervlakte van $$\Delta{ABC}$$ is op verschillende manieren te bereken. We kijken naar figuur 1.
2 manieren zijn:
De bach-stelling
Omdat je met beide manieren de oppervlakte berekent, zou je kunnen zeggen dat:
$$\frac{1}{2} · b · a $$ = $$\frac{1}{2} · c · h $$, oftewel b · a = c · h
Dit wordt ook wel de bach-stelling genoemd. Door de bekende getallen in te vullen kun je een van de variabelen berekenen.
Bijvoorbeeld b, a en c zijn bekend. Dan kun je door deze in te vullen, h berekenen.
Stel b = 2, a = 4, c = 4.
2 · 4 = 4 · h
4 · h = 8 $$ h = \frac{8}{4} = 2 $$
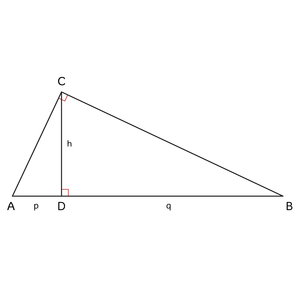
De hpq-stelling
In rechthoekige driehoeken is h2= p · q. Dit wordt de hpq-stelling genoemd.
Door deze in te vullen kun je h, p of q berekenen.
a. Zie Figuur 1. Bereken de hoogte LN in cm. Rond af op 1 decimaal.
b. Zie Figuur 2. Bereken PQ. Rond af op 1 decimaal.
Uitwerkingen:
a. bach-stelling: b · a = c · h
b = 7,5 ; a = 3,2 ; c = 8,2 ; h = LN
3,2 · 7,5 = 8,2 · LN.
24 = 8,2 · LN
$$LN = \frac{24}{8,2} = 2,9$$
b. hpq-stelling: h2= p · q, dus NQ2 = OQ · PQ
52 = 6,7 · PQ $$PQ = \frac {25}{6,7} = 3,7$$
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Daarnaast krijg je bij ieder fout gegeven antwoord direct een heldere uitleg hoe je de vraag het beste kunt oplossen. Zo leer je sneller en effectiever; dat is pas Slimleren!
Onderdeel worden van ons multidisciplinaire team? Dat kan! We zijn op zoek naar starters in de zorg, maar ook naar medisch specialisten en GZ-psychologen. Eén ding staat daarbij vast: je vult je functie anders in dan je gewend bent. Vind de vacature die bij je past en solliciteer!
Leren wordt leuker met Slimleren! Verzamel diamanten, speel mini-games en bereik gouden resultaten.
Slimleren is niet alleen leuker, maar ook veel goedkoper. Voor de prijs van 30 min bijles krijg je een hele maand Slimleren, al vanaf €8,95.
Met Slimleren houd je eenvoudig je voortgang bij en bereid je je optimaal voor op toetsen. Geen verrassingen meer!
Ervaar volledig adaptieve programma's door ons. Ons systeem speelt slim in op jouw uitdagingen. Leuker én effectiever leren!
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Onze programma's zijn gericht op leerlingen van groep 5 tot en met groep 8 van de basisschool en klas 1 tot en met klas 3 van de middelbare school. Of je nu wat moeite hebt met een bepaald vak, of juist vooruit wilt werken; Slimleren is er voor iedereen.
