Wil jij online oefenen met het onderwerp Basis - eigenschappen van hoeken? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!
Met Slimleren oefen je online op een leuke en efficiënte manier stof uit de les. Kom je ergens niet uit? Dan past het systeem automatisch het niveau aan en geeft handige tips. Zo loop je nooit meer vast en worden zelfs de moeilijkste onderwerpen een fluitje van een cent.
Hieronder zie je de theorie van het onderwerp Basis - eigenschappen van hoeken, met Slimleren kun je vragen over dit onderwerp (en honderden andere onderwerpen) oefenen. Je krijgt direct feedback als je een vraag fout beantwoordt en ziet gemakkelijk welke onderwerpen nog wat extra aandacht nodig hebben. Zo ben je altijd voorbereid op toetsen en ga je fluitend het schooljaar door.
In de wiskunde krijgen we te maken met hoeken van figuren. We willen deze kunnen berekenen om bepaalde informatie te verkrijgen over de figuur en alle onbekende variabelen uit te kunnen rekenen.
Wat de basis eigenschappen van hoeken zijn en hoe je hiermee kunt rekenen wordt in deze theorie behandeld. Denk aan termen als de hoekensom, basishoeken, overstaande hoeken, een gestrekte hoek, een rechte hoek en een volle hoek.
Hoeken kun je berekenen door gebruik te maken van de volgende regels:
De som van de 3 hoeken van een driehoek is 180°
∠A2 + ∠B + ∠C1 = 180°
De som van de 4 hoeken van een vierhoek is 360°
∠A + ∠B + ∠C + ∠D = 360°
De basishoeken van een gelijkbenige driehoek zijn gelijk
∠A1 = ∠B2
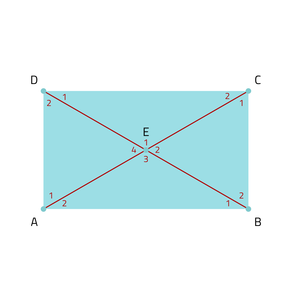
Overstaande hoeken zijn gelijk
∠E1 = ∠E3 en ∠E2 = ∠E4
Een volle hoek is 360°
∠E1 + ∠E2 + ∠E3 + ∠E4 = 360°
Een gestrekte hoek is 180°
∠E1 + ∠E2 = 180°
Een rechte hoek is 90°
∠A = ∠B = ∠C = ∠D = 90°
Bereken $$\angle{C}$$.
Uitwerking
De som van de hoeken van een driehoek zijn altijd 180° in totaal.
We kunnen hoek C dus berekenen door de resterende hoek te berekenen. $$\angle{C} = 180° - 110° - 40° = 30° $$
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Daarnaast krijg je bij ieder fout gegeven antwoord direct een heldere uitleg hoe je de vraag het beste kunt oplossen. Zo leer je sneller en effectiever; dat is pas Slimleren!
Onderdeel worden van ons multidisciplinaire team? Dat kan! We zijn op zoek naar starters in de zorg, maar ook naar medisch specialisten en GZ-psychologen. Eén ding staat daarbij vast: je vult je functie anders in dan je gewend bent. Vind de vacature die bij je past en solliciteer!
Leren wordt leuker met Slimleren! Verzamel diamanten, speel mini-games en bereik gouden resultaten.
Slimleren is niet alleen leuker, maar ook veel goedkoper. Voor de prijs van 30 min bijles krijg je een hele maand Slimleren, al vanaf €8,95.
Met Slimleren houd je eenvoudig je voortgang bij en bereid je je optimaal voor op toetsen. Geen verrassingen meer!
Ervaar volledig adaptieve programma's door ons. Ons systeem speelt slim in op jouw uitdagingen. Leuker én effectiever leren!
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Onze programma's zijn gericht op leerlingen van groep 5 tot en met groep 8 van de basisschool en klas 1 tot en met klas 3 van de middelbare school. Of je nu wat moeite hebt met een bepaald vak, of juist vooruit wilt werken; Slimleren is er voor iedereen.
