Uitdaging
Er zijn verschillende regels voor het berekenen van hoeken. Soms is een hoek te berekenen met de hulp van slechts 1 regel. Maar vaak worden meerdere regels achter elkaar gebruikt. Voordat je de juiste hoek kunt berekenen moeten soms andere hoeken worden berekend.
In deze theorie behandelen we kort de eigenschappen van hoeken die je kunt gebruiken om hoeken te berekenen en leggen we een nieuwe term uit: de bissectrice.
Methode
Je kent al verschillende regels om hoeken te berekenen:
- Een rechte hoek is 90°;
- Een gestrekte hoek is 180°;
- Een volle hoek is 360°;
- Overstaande hoeken zijn gelijk aan elkaar;
- In een gelijkbenige driehoek zijn de basishoeken gelijk aan elkaar;
- De drie hoeken van een driehoek zijn samen 180°;
- De vier hoeken van een vierhoek zijn samen 360°;
Een nieuwe regel is:
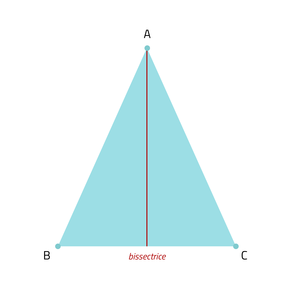
- Een bissectrice deelt een hoek precies middendoor. In de afbeelding wordt ∠A precies in tweeën gedeeld.
Als je hoeken berekent zet je altijd erachter welke regel(s) je hebt toegepast.