F-hoeken en Z-hoeken berekenen

Uitdaging

Misschien ken je inmiddels al een aantal regels die je gebruikt bij het berekenen van hoeken. Hier bespreken we er nog 2 die je goed kunt gebruiken.

Methode

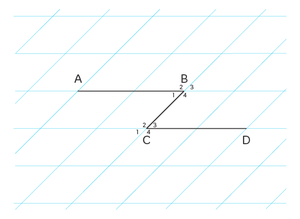
Z-hoeken

In figuren met evenwijdige lijnen kun je soms een Z herkennen. Dit zie je ook in de afbeelding genaamd Z-hoeken. De hoeken

$$\angle B_{1}$$ en $$\angle C_{3}$$ noem je Z-hoeken. Dit zijn de hoeken aan de binnenkant van de Z. Z-hoeken zijn altijd gelijk aan elkaar. Let wel op! De lijnen AB en CD in het figuur moeten evenwijdig (of parallel) aan elkaar lopen, anders zijn er geen Z-hoeken.

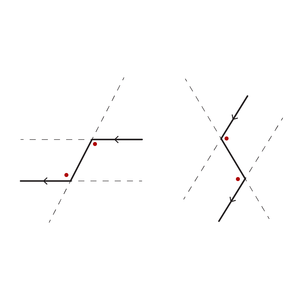
De Z-hoeken komen in verschillende vormen voor, twee andere voorbeelden zie je in de andere afbeelding.

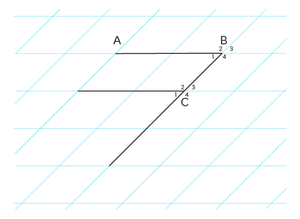
F-hoeken

Kijk naar de afbeelding F-hoeken. De hoeken

$$\angle B_{1}$$ en $$\angle C_{1}$$ zijn gelijk. Dit zijn namelijk F-hoeken. Net als Z-hoeken komen F-hoeken voor in figuren met twee evenwijdige lijnen en een lijn die deze evenwijdige lijnen snijdt of raakt. Ook F-hoeken komen in verschillende vormen voor.

Bewezen stellingen

Inmiddels ken je verschillende stellingen die je helpen bij het bereken van hoeken:

• Rechte hoek is 90°, gestrekte hoek is 180° en volle hoek is 360°
• Hoekensom driehoek = samen 180°
• Basishoeken zijn gelijk aan elkaar
• F-hoeken zijn gelijk aan elkaar
• Z-hoeken zijn gelijk aan elkaar
• Bissectrice deelt een hoek in twee gelijke hoeken.
• Z-hoeken en F-hoeken komen voor in figuren met twee evenwijdige lijnen en een lijn die deze evenwijdige lijnen snijdt of raakt.