Wil jij online oefenen met het onderwerp Grafieken verschuiven en veranderen? Of wil je andere wiskunde onderwerpen online oefenen? Dat kan op een leuke en leerzame manier met de oefensoftware van Slimleren. probeer Slimleren nu vrijblijvend een week gratis uit, en ontdek hoe makkelijk het werkt!
Met Slimleren oefen je online op een leuke en efficiënte manier stof uit de les. Kom je ergens niet uit? Dan past het systeem automatisch het niveau aan en geeft handige tips. Zo loop je nooit meer vast en worden zelfs de moeilijkste onderwerpen een fluitje van een cent.
Hieronder zie je de theorie van het onderwerp Grafieken verschuiven en veranderen, met Slimleren kun je vragen over dit onderwerp (en honderden andere onderwerpen) oefenen. Je krijgt direct feedback als je een vraag fout beantwoordt en ziet gemakkelijk welke onderwerpen nog wat extra aandacht nodig hebben. Zo ben je altijd voorbereid op toetsen en ga je fluitend het schooljaar door.
Grafieken kun je horizontaal en verticaal verschuiven, maar je kunt ze ook veranderen door te vermenigvuldigen. Als resultaat van het vermenigvuldigen zul je zien dat de grafiek verticaal uitrekt (of inkrimpt).
Hoe het verschuiven en het uitrekken of inkrimpen van een grafiek precies werkt leggen we je uit in deze theorie.
Je kunt een grafiek verticaal uitrekken door deze te vermenigvuldigen met een getal groter dan 1. De x-coördinaat blijft bij vermenigvuldiging altijd hetzelfde, maar de y-coördinaat wordt met het getal vermenigvuldigd.
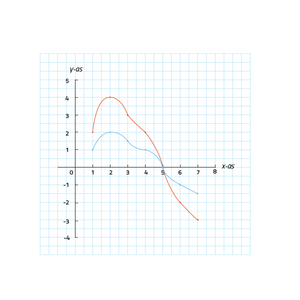
In de grafiek kun je zien wat er gebeurt als je de blauwe grafiek vermenigvuldigt met 2. Neem bijvoorbeeld punt A(1,1) op de blauwe grafiek. Op de nieuwe grafiek (de rode) blijft de x-coördinaat gelijk en de y-coördinaat wordt met 2 vermenigvuldigd. Het beeldpunt (op de nieuwe grafiek) wordt dan A'(1,2). Dit kun je voor alle punten in de grafieken nagaan.
Let op het punt B(5,0). Op de nieuwe grafiek is dit ook het beeldpunt B'(5,0) want de x-coördinaat blijft gelijk en de y-coördinaat wordt vermenigvuldigd met 2 en 0 · 2 = 0.
De beeldgrafiek kun je tekenen door dit voor alle coördinaten te doen en deze punten met elkaar te verbinden.
Door zo'n vermenigvuldiging verandert niet alleen de grafiek. De functie die bij de grafiek hoort verandert ook. Kijk maar eens naar dit voorbeeld: Neem als oorspronkelijke functie y = 2x2 +2x + 1. Als je de grafiek van deze functie vermenigvuldigt met 3, dan vermenigvuldig je ook de functie met 3. De functie van de beeldgrafiek wordt dan: y' = 3(2x2 +2x + 1). Je kunt hier de haakjes nog wegwerken: y' = 6x2 + 6x + 3.
Vergeet ook niet de rekenregels voor het verschuiven van een grafiek! (Weet je niet meer helemaal hoe dit werkt, kijk dan nog even bij de theorie over het verschuiven van een grafiek.)
a. Een grafiek heeft de formule f(x) = 2,5x3 , de nieuwe grafiek g(x) is 3 keer zo uitgerekt als f(x), schrijf de nieuwe formule op.
b. Wanneer de grafiek f(x) met 3 omlaag wordt verschoven en ook nog eens 5 naar links verschoven wordt en daarna wordt vermenigvuldigd met 3, krijg je grafiek h(x). Schrijf de nieuwe formule op.
Uitwerking
a. g(x) = 3 · (2,5x3) = 7,5x3
b. Je kunt bij deze vraag alle stappen in één keer in de formule aanpassen, maar voor het overzicht is het misschien makkelijk om het stap voor stap aan te pakken.
Je begint met de formule f(x) = 2,5x3
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Daarnaast krijg je bij ieder fout gegeven antwoord direct een heldere uitleg hoe je de vraag het beste kunt oplossen. Zo leer je sneller en effectiever; dat is pas Slimleren!
Onderdeel worden van ons multidisciplinaire team? Dat kan! We zijn op zoek naar starters in de zorg, maar ook naar medisch specialisten en GZ-psychologen. Eén ding staat daarbij vast: je vult je functie anders in dan je gewend bent. Vind de vacature die bij je past en solliciteer!
Leren wordt leuker met Slimleren! Verzamel diamanten, speel mini-games en bereik gouden resultaten.
Slimleren is niet alleen leuker, maar ook veel goedkoper. Voor de prijs van 30 min bijles krijg je een hele maand Slimleren, al vanaf €8,95.
Met Slimleren houd je eenvoudig je voortgang bij en bereid je je optimaal voor op toetsen. Geen verrassingen meer!
Ervaar volledig adaptieve programma's door ons. Ons systeem speelt slim in op jouw uitdagingen. Leuker én effectiever leren!
Met Slimleren oefen je online voor de vakken waar je nog wat moeite mee hebt, waar en wanneer je maar wilt. Theorie-uitleg, video-colleges, vuistregels en meer helpen jou om de stof sneller te begrijpen. Onze programma's zijn gericht op leerlingen van groep 5 tot en met groep 8 van de basisschool en klas 1 tot en met klas 3 van de middelbare school. Of je nu wat moeite hebt met een bepaald vak, of juist vooruit wilt werken; Slimleren is er voor iedereen.
