Uitdaging
Een trapezium is een vierhoek waarvan twee zijden evenwijdig zijn. Als de niet evenwijdige zijden even lang zijn heet zo'n trapezium een gelijkbenig trapezium. Een trapezium is dus ook een vierhoek, maarheeft slechts één paar evenwijdige zijdes.
In deze theorie bespreken we hoe we de oppervlakte van een trapezium kunnen berekenen.
Methode
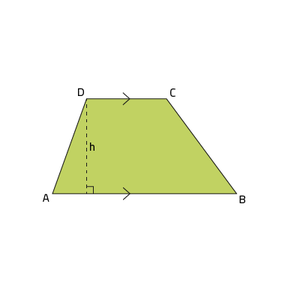
Een trapezium bestaat uit vier hoeken en minimaal één paar evenwijdige lijnen. De oppervlakte van een trapezium kun je als volgt berekenen:
- $$\mbox{Oppervlakte trapezium}= \frac{1}{2} · \mbox{ som evenwijdige zijden} · \mbox{ bijbehorende hoogte}$$
- Bijvoorbeeld in de afbeelding: $$\mbox{Oppervlakte } ABCD = \frac{1}{2} · (AB + CD) · h$$