Uitdaging
Een lichaamsdiagonaal in een balk is een lijn die vanuit een hoekpunt midden door de balk loopt naar een ander hoekpunt. We kunnen de lengte van deze lichaamsdiagonaal berekenen door gebruik te maken van de Stelling van Pythagoras.
In deze theorie leggen we je uit hoe dit werkt.
Methode
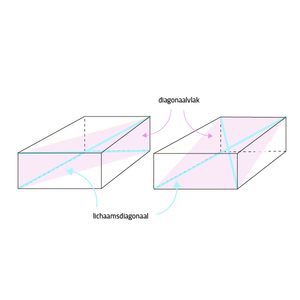
Iedere balk heeft altijd twee evenwijdige zijvlaksdiagnalen. Als we de balk op deze lijnen in gedachte doorsnijden, dan krijgen we een doorsnede van de balk die we het diagonaalvlak noemen. Zo'n diagonaalvlak is altijd een rechthoek.
Als je vervolgens in dit diagonaalvlak een diagonale lijn tekent (van lijn vanuit een hoek van dit diagonaalvlak naar de overstaande hoek in dit diagonaalvlak), dan noemen we die lijn een lichaamsdiagonaal. Deze lijn loopt namelijk als je naar de gehele balk kijkt, vanuit een hoekpunt midden door de balk naar een ander hoekpunt. Het is dus een diagonaal van het gehele lichaam.
Omdat het diagonaalvlak een rechthoek is, en daardoor in feite uit twee rechthoekige driehoeken bestaat, kunnen we de Stelling van Pythagoras gebruiken om de lengte van de lichaamsdiagnoaal uit te rekenen. Ook kunnen we de Stelling van Pythagoras gebruiken om de lengte van zijvlaksdiagonalen en ribben uit te rekenen.
De Stelling van Pythagoras is als volgt: $$a^2 + b^2 = c^2$$, waarbij a en b de rechthoekszijden zijn en c de schuine zijde is van de rechthoekige driehoek.
In de voorbeeldvraag laten we je zien hoe je de lengte van een lichaamsdiagonaal uitrekent in de praktijk.